Für technische Anwendungen wie CNC-und Roboterprogrammierung besteht Interesse, Bewegungsvorgaben, Bewegungsbahnen, aus Kreisen und Linien zusammenzusetzen. Interpolatoren in den CNC- und Robotersteuerungen bewegen Werkzeuge und Werkstücke nach solchen Vorgaben.
Eine Abfolge von Kreisbögen und Linien hat zumeist Knicke an den Übergängen zwischen zwei Segmenten. Mit Hilfe zirkularer Splines lassen sich Kurvenverläufe mit glatten Übergängen berechnen.
Biarcs sind eine Sonderform zirkularer Splines. Sie bestehen aus zwei Kreiselementen, Bi-Arcs, die tangential ineinander übergehen.
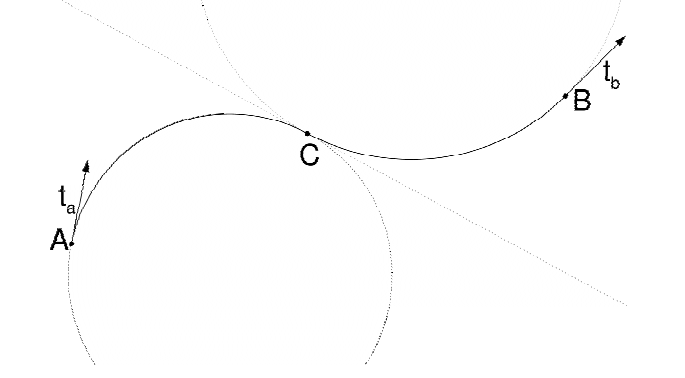
Ein Startpunkt A, ein Endpunkt B und die tangentialen Richtungsvektoren t_a, t_b in diesen Punkten beschreiben den Biarc. Diese Vorgaben kommen aus der Vorstellung über den Kurvenverlauf.
Ein mathematisches Problem besteht in der Berechnung eines geeigneten Berührpunktes C der beiden Kreissegmente.
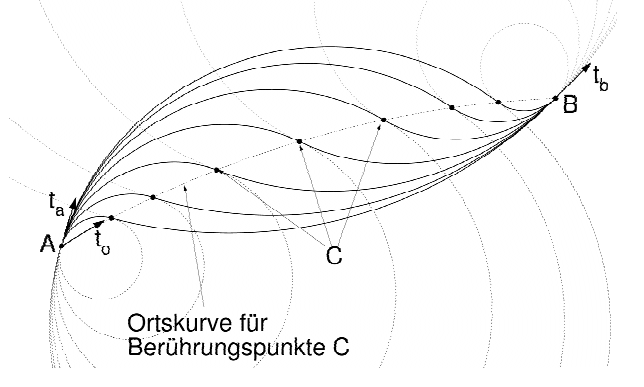
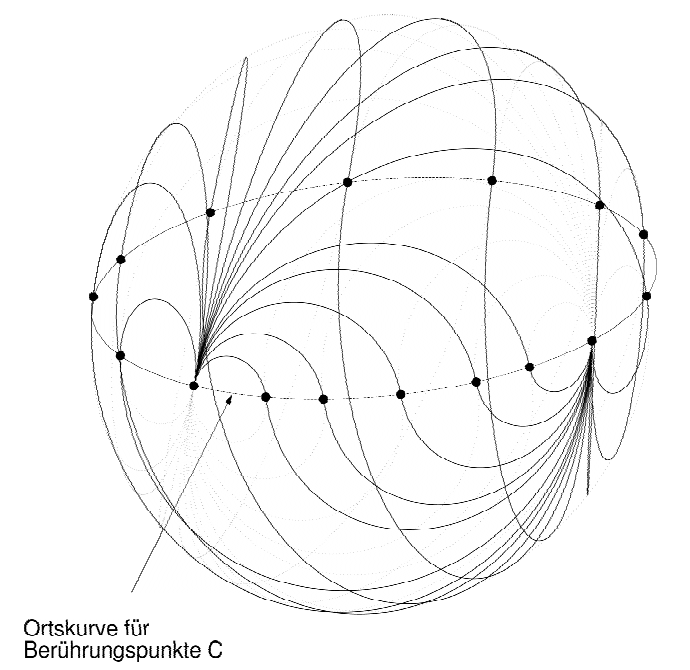
Unsere Lösung setzt die geometrische Anordnung konsequent in Vektorrechnung um. Sie löst die Suche geeigneter Berührpunkte in der Ebene (2-D) und im Raum (3-D).
Die Implementierung erfolgte in ANSI-C und kann auf Computern und auf Microcontrollern eingesetzt werden.
technische Referenz:
Erich Kohlhaas, Offline-Programmierung von Industrierobotern
Fortschritt-Bericht VDI, Reihe 8, Nr. 716, VDI-Verlag 1998, ISBN 3-18-371608-9