Motivation und Lösungskonzept an einem einfachen Beispiel
Auf dieser Seite betrachten wir die klassische Ausgleichsrechnung anhand eines einfachen Beispieles, dem Ohm’schen Gesetz.
Das Ohm’sche Gesetz ist ein einfaches Modell. Es beinhaltet drei Variablen, die Spannung U, die Stromstärke I und den Widerstand R.
\[ U=R\cdot I\]Typischerweise erhält man die Spannung \( U \) und die Stromstärke \(I\) durch Messungen an einem Aufbau und möchte aus den gemessenen Daten einen unbekannten Widerstand \( R \) berechnen. Die einfachste Art das zu tun ist durch das Umformen der Gleichung und darauf folgendes Einsetzen von Messwerten.
- Umstellen der Gleichung
\[ R = \frac{U}{I} \] - Aus den Messwerten \[ U= 4.98 \mbox{V}\\ I = 2.01 \mbox{mA} \] ergibt sich
\[ R = \frac{U}{I} = \frac{4.98 \mbox{V}}{2.01 \mbox{mA}} = 2.4653 \mbox{k}\Omega \]
Bei dieser Art der Berechnung des Widerstandes werden allerdings nur die Werte einer einzigen Messung betrachtet. Messfehlern, Störungen oder andere Ungenauigkeiten können aber dazu führen dass der tatsächliche Wert erheblich abweicht.
Um diesen möglichen Fehler zu minimieren, gibt es unterschiedliche Vorgehensweisen. Die bekannteste ist die Minimierung der Fehlerquadrate mittels Ausgleichrechnung.
Bei der Ausgleichsrechnung wird nicht nur eine einzige Messung, sondern eine Messreihe, also eine Sammlung vieler Messungen an demselben Aufbau, betrachtet. Hierbei ist es wichtig darauf zu achten, dass die gemachten Messungen unabhängig voneinander sind.
Die Tabelle zeigt einen Datensatz bestehend aus sechs einzelnen Messungen.
| Index \( i \) | 1 | 2 | 3 | 4 | 5 | 6 |
| \( \frac{U}{\mbox{V}} \) | -5,03 | -2,99 | -1,00 | 0,99 | 3,02 | 4,98 |
| \( \frac{I}{\mbox{mA}} \) | -2,03 | -1,24 | -0,41 | 0,4 | 1,21 | 2,01 |
Die Ausgleichsrechnung basiert auf dem Minimieren von Restfehlern, auch Residuen genannt.
- Ausgehend von einem einzelnen Fehlerterm
\[ \Delta_i = U_i – R\cdot I_i \]
wird der Wert \( R \) gesucht, der die Summe aller Fehlerquadrate minimiert. - \[ V = \sum_i \Delta_i^2 \]
Die Summe läuft über alle Werte der Messreihe. - Um das Minimum zu erhalten wird die Summe nach der Unbekannten abgeleitet und die Ableitung Null gesetzt.
\[ \frac{\partial{V}}{\partial{R}} = 0 \]
Mit Einsetzen und Kettenregel ergibt sich:
\[ \frac{\partial{V}}{\partial{R}} = \frac{\partial{\sum_i \Delta_i^2}}{\partial{R}} = 2 \sum_i \frac{\partial{\Delta_i}}{\partial{R}} \Delta_i \] - und nach Einsetzen von
\[ \frac{\partial{\Delta_i}}{\partial{R}} = \frac{\partial{ \left( U_i – R \cdot I_i \right) }}{\partial{R}} = \frac{\partial{ U_i }}{\partial{R}} – \frac{\partial{ R \cdot I_i }}{\partial{R}}= 0 – 1 \cdot I_i = – I_i \] - und Nullsetzen folgt eine Gleichung
\[ 2 \sum_i \left[ -I_i \left( U_i- R \cdot I_i \right) \right] = 2 \left( -\sum_i U_i I_i + R \sum_i I_i^2 \right)= 0 \] - Durch Umstellen ergibt sich
\[ \sum_i U_i I_i = R \cdot \sum_i I_i^2 \]
und aufgelöst findet man das optimale, das beste \( R \) zu diesen Messdaten als
\[ R = \frac{\sum_i U_i I_i}{\sum_i I_i^2} \]
Diese Gleichung beschreibt den gesuchten optimalen Wert für den Widerstand \( R \).
Statt mit einem Taschenrechner führen wir die Berechnung in einem kleinem Python 3 Programm aus. Dabei benutzen wir mit numpy und mathplotlib weit verbreitete Hilfsmittel.
# typische Libraries
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.use("Agg") # Matplotlib soll Agg verwenden und nur Dateien generieren
def CalcR( U, I):
if len(U) != len(I):
print("Error: Daten haben unterschiedliche Längen")
return None # Abbruch
# Speicher für die Teilsummen
sum_ui=0.0
sum_i2=0.0
for cnt in range(len(U)):
sum_ui+=U[cnt]*I[cnt]
sum_i2+=I[cnt]*I[cnt]
if sum_i2<0.0001: return None # Division durch 0 abfangen
R=sum_ui/sum_i2
return R
if __name__ == '__main__':
# Unsre Daten
U=[-5.03,-2.99,-1.00, 0.99, 3.02, 4.98]
I=[-2.03,-1.24,-0.41, 0.40, 1.21, 2.01]
# Berechnung aufrufen
R=CalcR(U,I)
# Ergebnis drucken
print("R = {} kOhm".format(R))
# Eine Graphik erstellen
fig, ax = plt.subplots()
U_est=[]
for i in I:
U_est.append(R*i)
ax.plot(I, U_est, '-')
ax.plot(I, U, 'o', color='tab:brown')
plt.xlabel('Strom I in mA')
plt.ylabel('Spannung U in V')
plt.savefig("R_Plot.png", dpi=300)
Lässt man den Code laufen erhält man als Ergebnis:
"R = 2.470541650711874 kOhm"
und die Datei "R_Plot.png" im Arbeitsverzeichnis zeigt folgendes Bild
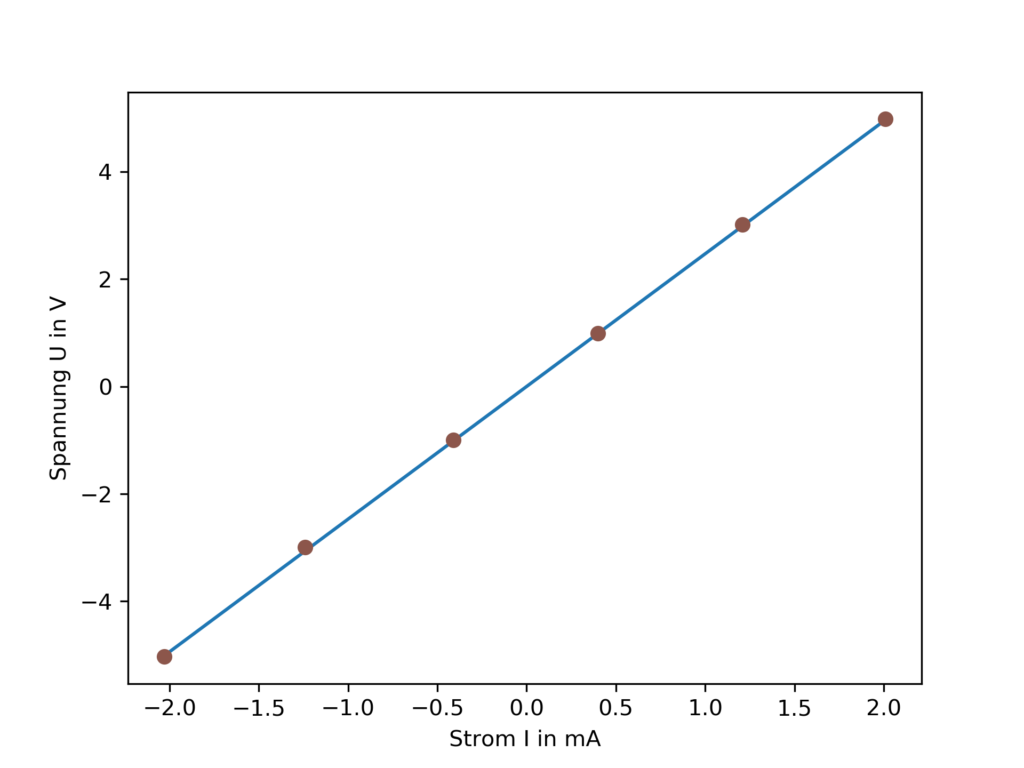
Die hier sichtbaren roten Punkte stellen die Werte der Messreihe dar, die blaue Linie die Modell-Kurve mit dem berechneten Widerstandswert. Es ist zu erkennen, dass nicht alle Messwerte exakt auf der Linie liegen, aber es gibt auch keine andere Linie die näher an den angezeigten Werten liegt.
Verändern Sie doch die Messwerte und spielen Sie mit dem erarbeiteten Programm!
Erweiterung auf zwei Freiheitgrade
Das bisher betrachtete Modell, hat einen unbekannten Wert der zu bestimmen ist, und damit einen Freiheitsgrad. Wir erweitern das Modell um einen weiteren Freiheitsgrad, einen Spannungsoffset \( U_0 \) , und führen erneut die Ausgleichrechnung durch.
Das erweiterte Modell lautet:
- Damit ergibt sich die Abweichung für jede EInzelmessung:
\[ \Delta_i = U_i - R\cdot I_i - U_0 \] - Es gibt zwei Parameter \( R \) und \( U_0 \) in jeder Abweichung. Diese sollen aus der Minimierung des Fehlerquadraten bestimmt werden.
\[ V = \sum_i \Delta_i^2 \] - Nun ergeben sich zwei Gleichungen aus der Ableitung des Fehlerquadrates nach den Parametern:
\[ \frac{\partial{V}}{\partial{R}} = 0 \]
[ \frac{\partial{V}}{\partial{U_0}} = 0 ] - Man erhält nach der Kettenregel:
\[ 2 \sum_i \frac{\partial{\Delta_i}}{\partial{R}} \Delta_i = 0 \]
\[ 2 \sum_i \frac{\partial{\Delta_i}}{\partial{U_0}} \Delta_i = 0 \] - mit
\[ \frac{\partial{\Delta_i}}{\partial{R}} = \frac{\partial{ \left( U_i - R \cdot I_i - U_0 \right) }}{\partial{R}} = - I_i \]
\[ \frac{\partial{\Delta_i}}{\partial{U_0}} = \frac{\partial{ \left( U_i - R \cdot I_i - U_0 \right) }}{\partial{U_0}} = 1 \] - und Nullsetzen folgt ein 2x2 Gleichungssystem
\[ 2 \sum_i \left[ -I_i \left( U_i- R \cdot I_i -U_0\right) \right] = 2 \left( -\sum_i U_i I_i + R \sum_i I_i^2 + U_0\sum_i I_i\right)= 0 \]
\[ 2 \sum_i \left[ -1\cdot \left( U_i- R \cdot I_i -U_0\right) \right] = 2 \left( -\sum_i U_i + R \sum_i I_i + U_0 \sum_i 1 \right)= 0 \] - Das Dleichungsystem wird noch etwas umsortiert
\[ \sum_i U_i I_i = R \cdot \sum_i I_i^2 + U_0\cdot\sum_i I_i\]
\[ \sum_i U_i = R \cdot \sum_i I_i+ U_0\cdot\sum_i 1 \] - und die Lösung wird etwa mit der Cramer'schen Regel bestimmt zu
\[ R = \frac{\sum_i U_i I_i \cdot \sum_i 1 - \sum_i U_i \cdot \sum_i I_1}{\sum_i I_i^2 \cdot \sum_i 1 - \sum_i I_i \cdot\sum_i I_i } \]
\[ U_0 = \frac{\sum_i I_i^2 \cdot \sum_i U_i -\sum_i I_i\cdot \sum_i U_i I_i}{\sum_i I_i^2 \cdot \sum_i 1 - \sum_i I_i \cdot\sum_i I_i } \] - oder mit \( n = \sum_i 1 \) die ANzahl der Messpunkte
\[ R = \frac{n \sum_i U_i I_i - \sum_i U_i \cdot \sum_i I_1}{n \sum_i I_i^2 - \left(\sum_i I_i \right)^2 } \]
\[ U_0 = \frac{\sum_i I_i^2 \cdot \sum_i U_i -\sum_i I_i\cdot \sum_i U_i I_i}{n \sum_i I_i^2 - \left(\sum_i I_i \right)^2 } \]
Auch wenn dieser Ausdruck komplizierter aussieht als oben. Die Umsetzung der Summen und das Ausrechnen der gesuchten Größen lässt sich leicht in Python oder einer anderen Programmiersprache umsetzen. Hierzu der angepasste Sourcecode in Python. Er liefert das Ergebnis.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Beispiel zur Ausgleichsrechnung
Bestimmung des Widerstandes R aus einer Messreihe U_i und I_i
"""
#
# typische Libraries, die wir oft brauchen.
#
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.use("Agg") # Matplotlib soll Agg verwenden und nur Dateien generieren
def CalcRU0( U, I):
if len(U) != len(I):
print("Error: Daten haben unterschiedliche Längen")
return None # Abbruch
#
# Speicher für die Teilsummen
sum_ui=0.0
sum_u=0.0
sum_i2=0.0
sum_i=0.0
n =len(U)
for cnt in range(n):
sum_ui+=U[cnt]*I[cnt]
sum_u+=U[cnt]
sum_i2+=I[cnt]*I[cnt]
sum_i+=I[cnt]
det= n * sum_i2 - sum_i*sum_i
if det<0.0001: return None # Division durch 0 abfangen
R=(n*sum_ui-sum_u*sum_i)/det
U_0=(sum_i2*sum_u-sum_i*sum_ui)/det
return R,U_0
#
# Falls diese Datei gestartet wurde, ...
# ( Sonst können wir die Berechnung in einen
# anderen Programm wiederverwenden )
if __name__ == '__main__':
#
# Unsre Daten
#
U=[-5.03,-2.99,-1.00, 0.99, 3.02, 4.98]
I=[-2.03,-1.24,-0.41, 0.40, 1.21, 2.01]
#
# Berechnung aufrufen
#
R, U_0=CalcRU0(U,I)
#
# Ergebnis drucken
#
print("R = {} kOhm".format(R))
print("U_0 = {} V".format(U_0))
#
# Eine Graphik erstellen
#
fig, ax = plt.subplots()
U_est=[]
for i in I:
U_est.append(R*i + U_0 )
ax.plot(I, U_est, '-')
ax.plot(I, U, 'o', color='tab:brown')
plt.xlabel('Strom I in mA')
plt.ylabel('Spannung U in V')
plt.savefig("R_U0_Plot.png", dpi=300)
Er liefert auf der Console das Ergebnis
R = 2.470644549268073 kOhm
U_0 = 0.01970644549268085 V
und generiert das Bild "R_U0_Plot.png"
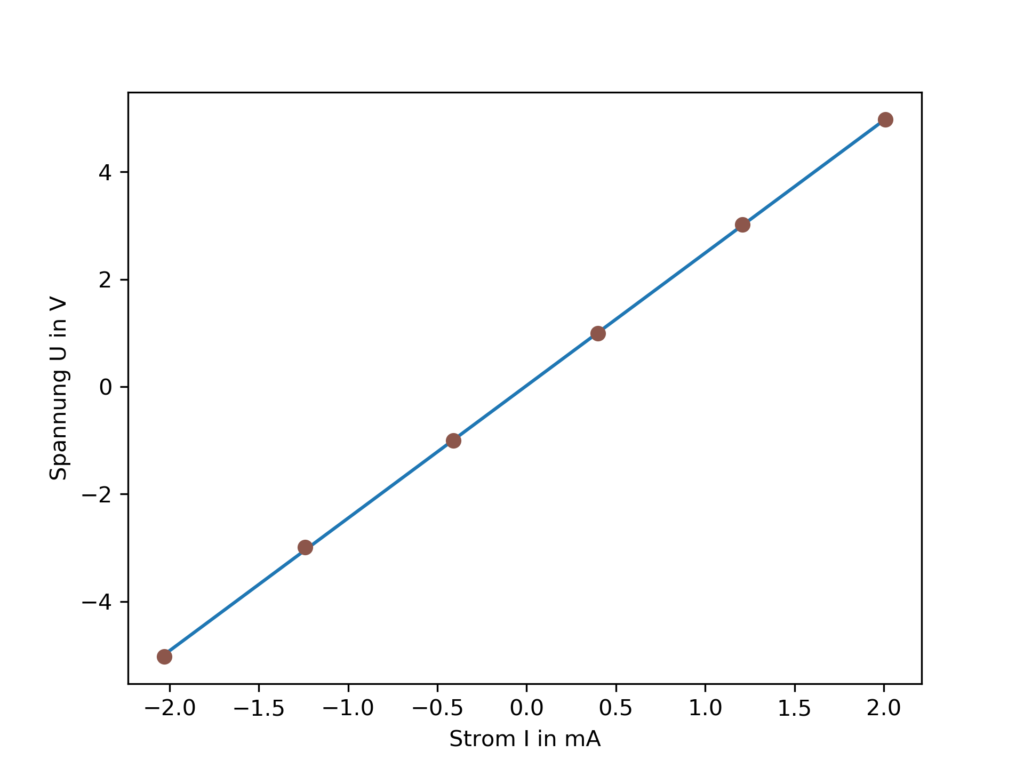
R_U0_Plot.png